29 March 2024

Aniruddha Rajendra RAO
Research & Development Division
Hitachi America, Ltd.
The global datasphere is growing at an unprecedented rate, with predictions that it will reach 175 zettabytes by 2025[1] but as a 2021 MIT Technology Review notes, we’re just “scratching the surface of data-driven opportunities.”[2] This presents exciting opportunities for data scientists, but it also raises challenges in terms of efficiently storing, transferring, and computing such vast amounts of data. Dimension reduction is a crucial technique in addressing these challenges, as it allows for the reduction of input variables while preserving meaningful data. In this blog article, we explore the limitations of existing dimension reduction methods and introduce a novel and effective approach using Functional Data Analysis (FDA) and Bi-Functional Autoencoders (BFAE).
Traditional machine learning methods for dimension reduction, such as principal component analysis (PCA) and autoencoders (AE), are not well-suited for time series data. These methods are designed to work with data recorded at regularly spaced intervals in a finite-dimensional space, and they struggle to capture the complex relationships within time series data. More promising methods, like functional principal component analysis (FPCA) and functional autoencoders (FAE), have their limitations as well. FPCA only learns a linear representation of the data, which is inadequate for cases where the underlying mapping is complex. FAE, on the other hand, offers a latent representation of functional data in scalar form, which fails to capture the complex relations of the functional features.
To overcome the limitations of existing methods, my colleagues and I at Hitachi America R&D have been investigating a novel approach using FDA and BFAE. (See Fig. 1 below for the general architecture.) BFAE offers a general functional mapping from multivariate temporal variables to themselves, preserving the functional nature of the data. This approach captures non-linear relationships while reducing dimensions in terms of both features and time points. By utilizing both a functional encoder and a functional decoder, our approach provides flexibility in transforming the data into low-dimensional latent representations. This flexibility allows for different analytical tasks such as prediction, classification, clustering, and forecasting.
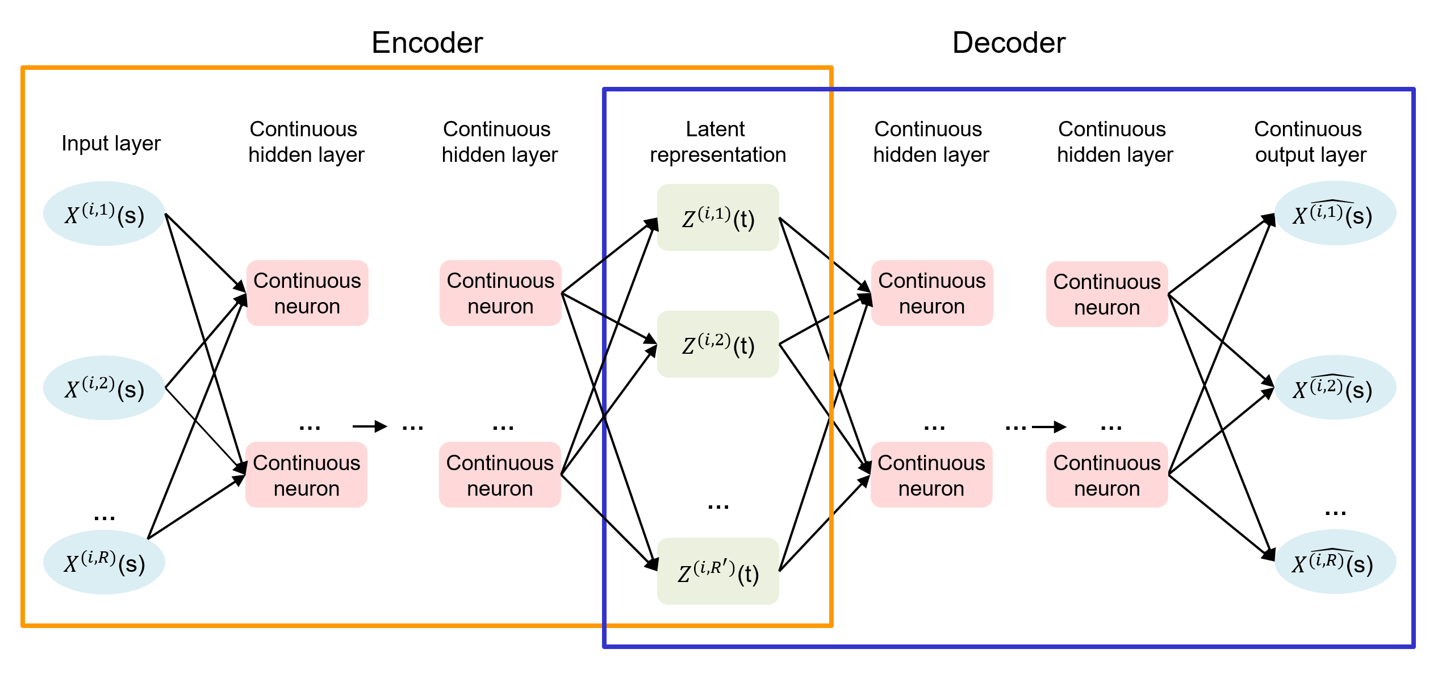
Figure 1. General architecture of the bi-functional autoencoder
We conducted simulations to compare the performance of BFAE with other methods. The results showed that our approach outperforms other methods, especially with larger sample sizes and higher numbers of time points. Even when representing curves with only 10 time points, our approach still outperformed others in capturing the shape of the curve.
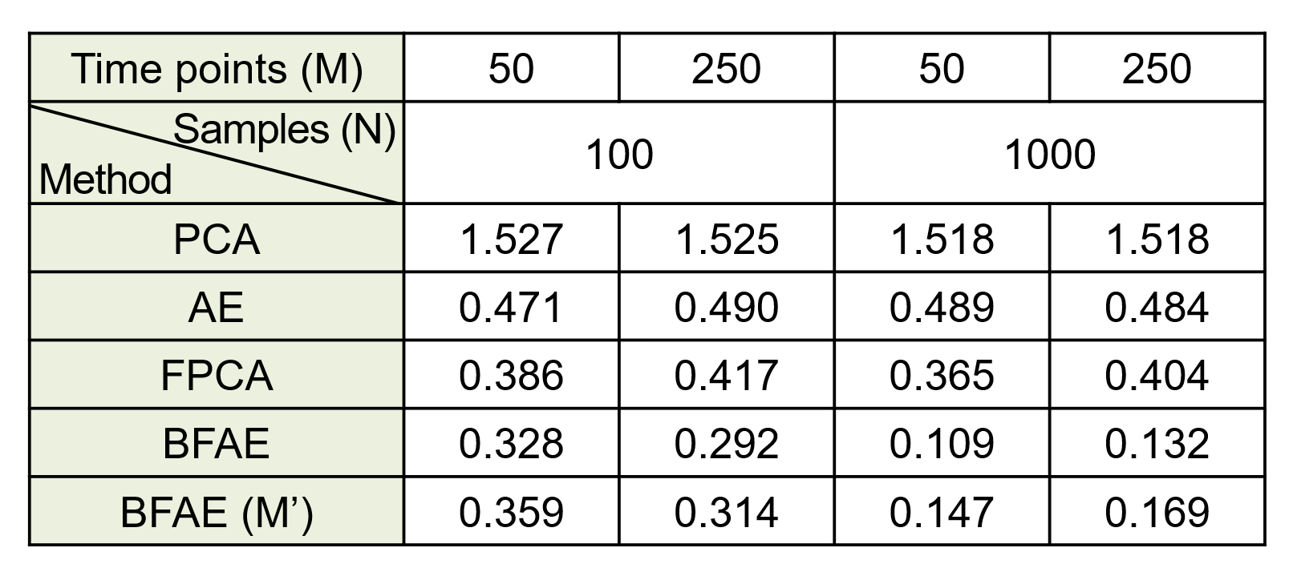
Table I: Comparing RMSE of different methods for capturing multiple (R = 10) time series function
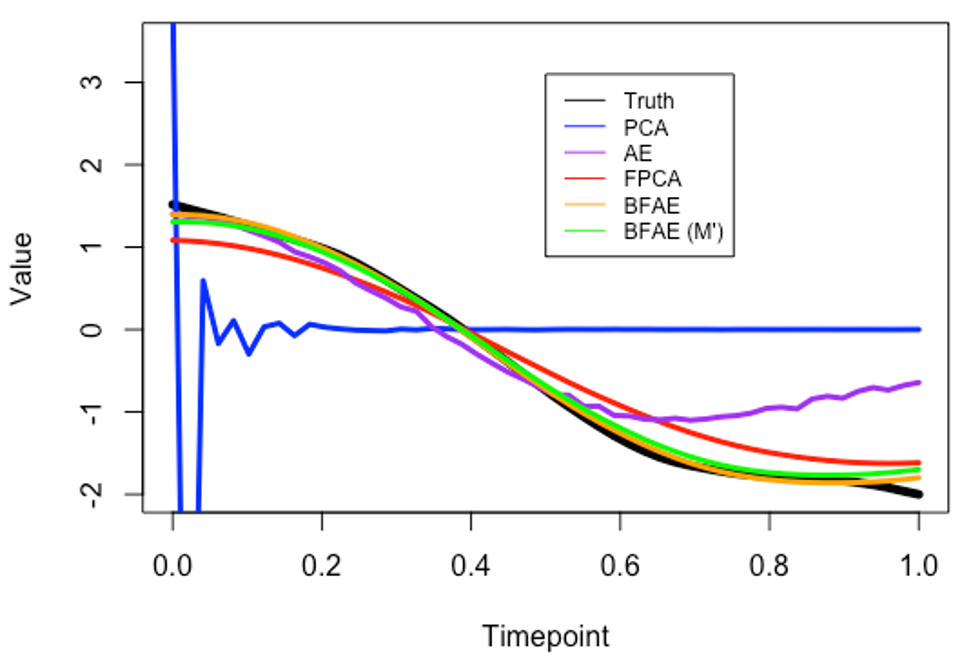
Figure 2. Comparison of the curve reconstruction (N = 1000, R = 1, and M = 50) for the different methods
We then looked at real-world examples to compare the performance of BFAE with other methods. One example involved speech recognition data, where BFAE outperformed other methods in capturing voice signal curves (Figure 2). Another example focused on the relationship between electricity demand and temperature (Figure 3), where BFAE effectively reduced the dimension without loss of important information.
Table II: Comparison of prediction performance using RMSE for the different methods based on real-world examples
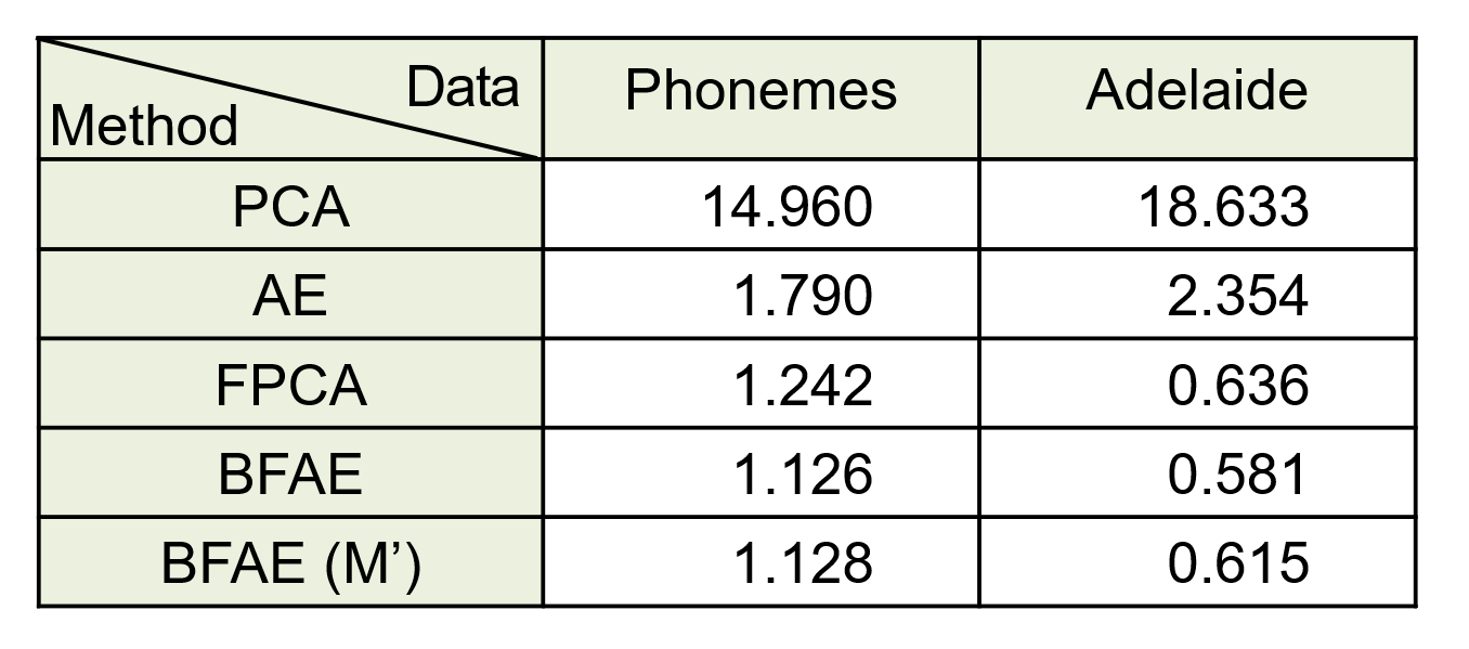
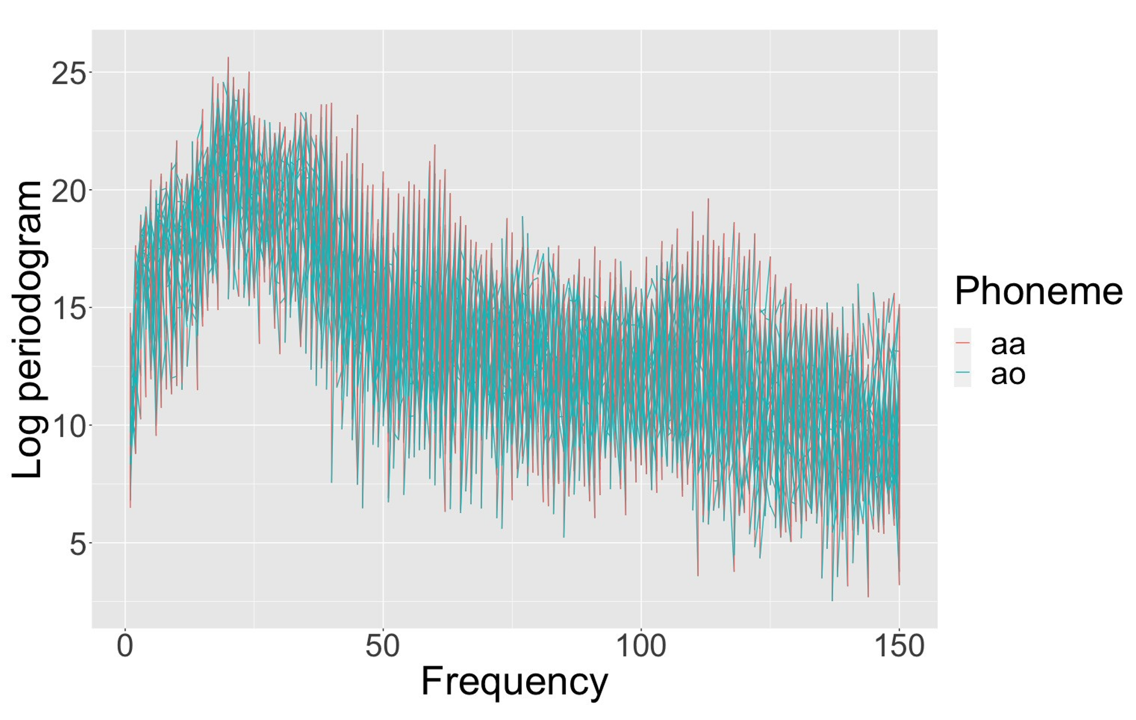
Figure 3. Voice signal curves for the phonemes data
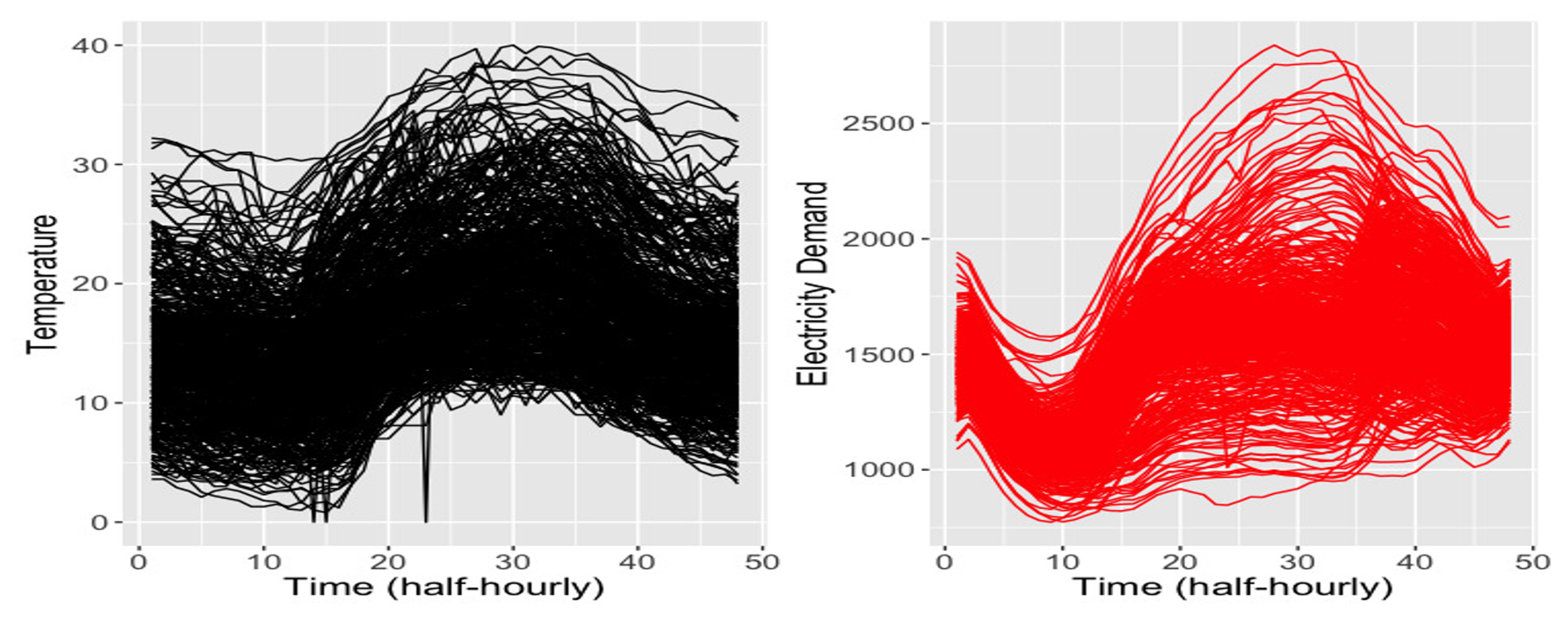
Figure 4. Time curves of temperature and electricity demand
Our proposed approach offers several advantages over existing methods. Firstly, it maintains the functional nature of the data throughout the construction process, resulting in a richer structure for transforming the data into low-dimensional latent representations. Secondly, it provides flexibility in representing time series data while capturing correlations and complex relations among features. Lastly, it helps in reducing dimensions in terms of both features as well as time points. The simulations and real-world examples demonstrated that our approach produced smaller errors in reconstruction and effectively modeled the data.
In conclusion, the rapid growth of the global datasphere presents challenges in terms of efficiently storing, transferring, and computing vast amounts of data. Dimension reduction is a crucial technique in addressing these challenges, and our proposed approach using BFAE offers a novel and effective solution. By preserving the functional nature of the data and capturing non-linear relationships, our approach reduces dimensions in terms of both features and time points while retaining performance. We invite readers to explore the details of our research in the original research paper, "A Functional approach for Two Way Dimension Reduction in Time Series" presented at the 2022 IEEE International Conference on Big Data.
I’d like to thank Dr. Haiyan Wang and Dr. Chetan Gupta, co-authors of the research paper, for their support in preparing this blog article.